
June Huh in his Princeton University office. Caroline Gutman for Quanta Magazine
une Huh often finds himself lost. Every afternoon, he takes a long walk around Princeton University, where he’s a professor in the mathematics department. On this particular day in mid-May, he’s making his way through the woods around the nearby Institute for Advanced Study — “Just so you know,” he says as he considers a fork in the path ahead, “I don’t know where we are” — pausing every so often to point out the subtle movements of wildlife hiding beneath leaves or behind trees. Among the animals he spots over the next two hours of wandering are a pair of frogs, a red-crested bird, a turtle the size of a thimble, and a quick-footed fox, each given its own quiet moment of observation.
“I’m very good at finding stuff,” he says. “That’s one of my special abilities.”
Huh, 39, has now been awarded the Fields Medal, the highest honor in mathematics, for his ability to wander through mathematical landscapes and find just the right objects — objects that he then uses to get the seemingly disparate fields of geometry and combinatorics to talk to each other in new and exciting ways. Starting in graduate school, he has solved several major problems in combinatorics, forging a circuitous route by way of other branches of math to get to the heart of each proof. Every time, finding that path is akin to a “little miracle,” Huh said.
One might say the same of his path into mathematics itself: that it was characterized by much wandering and a series of small miracles. When he was younger, Huh had no desire to be a mathematician. He was indifferent to the subject, and he dropped out of high school to become a poet. It would take a chance encounter during his university years — and many moments of feeling lost — for him to find that mathematics held what he’d been looking for all along.
That poetic detour has since proved crucial to his mathematical breakthroughs. His artistry, according to his colleagues, is evident in the way he uncovers those just-right objects at the center of his work, and in the way he seeks a deeper significance in everything he does. “Mathematicians are a lot like artists in that really we’re looking for beauty,” said Federico Ardila-Mantilla, a mathematician at San Francisco State University and one of Huh’s collaborators. “But I think in his case, it’s really pronounced. And I just really like his taste. He makes beautiful things.”
“When I found out that he came to mathematics after poetry, I’m like, OK, this makes sense to me,” Ardila added.
Huh himself draws parallels between the artist and the mathematician. For both, he said, “it feels like you’re grabbing something that’s already there, rather than creating something in your mind.”
The Dropout
On any given day, Huh does about three hours of focused work. He might think about a math problem, or prepare to lecture a classroom of students, or schedule doctor’s appointments for his two sons. “Then I’m exhausted,” he said.
“Doing something that’s valuable, meaningful, creative” — or a task that he doesn’t particularly want to do, like scheduling those appointments — “takes away a lot of your energy.”
To hear him tell it, he doesn’t usually have much control over what he decides to focus on in those three hours. For a few months in the spring of 2019, all he did was read. He felt an urge to revisit books he’d first encountered when he was younger — including Meditations by the Roman emperor Marcus Aurelius and several novels by the German author Hermann Hesse — so that’s what he did. “Which means I didn’t do any work,” Huh said. “So that’s kind of a problem.” (He’s since made peace with this constraint, though. “I used to try to resist … but I finally learned to give up to those temptations.” As a consequence, “I became better and better at ignoring deadlines.”)

Huh’s notes from a recent lecture. Caroline Gutman for Quanta Magazine
He finds that forcing himself to do something or defining a specific goal — even for something he enjoys — never works.
It’s particularly difficult for him to move his attention from one thing to another. “I think intention and willpower … are highly overrated,” he said. “You rarely achieve anything with those things.”
This has been the case since he was young. He was born in 1983 in California, where his parents were finishing graduate school. The family then moved to Seoul, South Korea, when Huh was around 2 years old. There, his father taught statistics, his mother Russian language and literature.
School was excruciating for him. He loved to learn but couldn’t focus or absorb anything in a classroom setting. Instead, he preferred to read on his own — in elementary school, he devoured all 10 volumes of an encyclopedia about living things — and to explore a mountain near his family’s apartment. He quickly became familiar with every corner of it, but he still managed to get lost, one time even ending up in an area that was restricted due to the possible presence of land mines.
He tried his best to avoid math whenever possible. His father once tried to teach him out of a workbook, but rather than try to solve the problems, Huh would copy the solutions from the back. When his father caught on and tore those pages out, Huh went to a local bookstore and wrote down the answers there. “He gave up at that point,” Huh said.
When he was 16 years old and in the middle of his first year in high school (which lasts for three years in South Korea), he decided to drop out to write poetry. He was something of a romantic. “I could literally physically cry after listening to good music,” he said. He wrote about nature and about his own experiences. He planned to complete his masterpiece in the two years before he’d have to attend university. “So that didn’t happen,” he laughed.
He found the writing process too focused on the self — and for him, that exploration was often painful and depressing. Moreover, as he later realized, “I wanted to be someone who writes great poetry,” he said. “I didn’t want to write great poetry.” Now he sees that version of himself as almost a complete stranger.
When he entered Seoul National University in 2002, he felt adrift. He briefly flirted with the idea of being a science writer and decided to major in astronomy and physics. But he frequently skipped class, and he had to retake several courses. “I was just generally lost,” he said. “I didn’t know what I wanted to do. I didn’t know what I was good at.”
It turned out that he was good at math after all — something he discovered entirely by accident.
True Beauty
It took Huh six years to graduate. In that sixth year, he enrolled in a class taught by the famed Japanese mathematician Heisuke Hironaka, who won the Fields Medal in 1970. Hironaka was charismatic, and Huh quickly fell under his sway.
But it wasn’t just his professor’s charm that attracted Huh that first day in class. It was also the math itself. Ostensibly, the course was an introduction to algebraic geometry, the study of solutions to algebraic equations and their geometric properties. Instead, Hironaka taught his own work in an area called singularity theory, which focuses on certain types of spaces. “Basically, he lectured about what he thought about yesterday,” Huh said — a very particular problem, and proofs that weren’t necessarily correct. What began as a 200-student class quickly dwindled; a few weeks later, only five students were left, Huh among them.
For the first time, he witnessed research mathematics unfolding in real time. Hironaka’s lectures weren’t polished as in other undergraduate courses, where everything was streamlined, the answers already worked out. Huh loved the suspense of it, the act of trying to do something no one really knew how to do — and the freedom that came with not knowing, the surprises that became possible. The typical material taught in college has been refined over the course of centuries, he said. “That’s very different from observing this raw mathematics in front of your eyes.”

Huh on the Princeton University campus. Caroline Gutman for Quanta Magazine
Huh discovered that this kind of mathematics could give him what poetry could not: the ability to search for beauty outside himself, to try to grasp something external, objective and true, in a way that opened him up more than writing ever had. “You don’t think about your small self,” he said. “There’s no place for ego.” He found that unlike when he was a poet, he was never motivated by the desire for recognition. He just wanted to do math.
Hironaka, perhaps recognizing this, took him under his wing. After Huh graduated and started a master’s program at Seoul National University — where he also met Nayoung Kim, now his wife — he spent a lot of time with Hironaka. During breaks, he followed the professor back to Japan, staying with him in Tokyo and Kyoto, carrying his bags, sharing meals, and of course continuing to discuss math.
An Unexpected Discovery
Huh applied to about a dozen doctoral programs in the U.S. But because of his undistinguished undergraduate experience, he was rejected by all of them save one. In 2009, he began his studies at the University of Illinois, Urbana-Champaign, before transferring to the University of Michigan in 2011 to complete his doctorate.
Despite the challenges — living in a new country, spending time apart from Kim (she stayed at Seoul National University for her doctorate in mathematics) — Huh cherished his experiences in graduate school. He was able to dedicate himself wholly to math, and he relished the freedom of exploration that had drawn him to the subject in the first place.
He immediately stood out. As a beginning graduate student in Illinois, he proved a conjecture in graph theory that had been open for 40 years. In its simplest form, the problem, known as Read’s conjecture, concerned polynomials — equations like n4 + 5n3 + 6n2 + 3n + 1 — attached to graphs, which are collections of vertices (points) connected by edges (lines). In particular, let’s say you want to color the vertices of a graph so that no two adjacent vertices have the same color. Given a certain number of colors at your disposal, there are many ways to color the graph. It turns out that the total number of possibilities can be calculated using an equation called the chromatic polynomial (which is written in terms of the number of colors being used).
Mathematicians observed that the coefficients of chromatic polynomials, no matter the graph, always seem to obey certain patterns. First, they are unimodal, meaning they increase and then decrease. Take the previous example of a polynomial. The absolute values of its coefficients — 1, 5, 6, 3, 1 — form a unimodal sequence. Moreover, that sequence is also “log concave.” For any three consecutive numbers in the sequence, the square of the middle number is at least as large as the product of the terms on either side of it. (In the above polynomial, for instance, 62 ≥ 5 × 3.)
Still, mathematicians struggled to prove these properties. And then, seemingly out of nowhere, along came Huh.
As a master’s student, he had studied algebraic geometry and singularity theory with Hironaka. The main objects of study in that field are called algebraic varieties, which can be thought of as shapes defined by certain equations. Intriguingly, associated to certain kinds of algebraic varieties are numbers that are known to be log concave — something Huh only knew because of the serendipitous direction his studies had taken him in. Huh’s key idea was to find a way to construct an algebraic variety such that those associated numbers were precisely the coefficients of the chromatic polynomial of the graph from the original question.
His solution stunned the math community. It was at that point that the University of Michigan, having rejected his initial application, recruited him to their graduate program.
Huh’s achievement was impressive not just because he had solved Read’s conjecture when it had seemed completely intractable for so long. He had shown that something much deeper — and geometric — was lurking beneath combinatorial properties of graphs.
Mathematicians were also impressed by his demeanor. His talks at conferences were always accessible and concrete; in speaking with him, it was clear that he was thinking both deeply and broadly about the concepts he was working with. “He was ridiculously mature for a graduate student,” said Matthew Baker, a mathematician at the Georgia Institute of Technology. After Baker met him for the first time, “I was just like, who is this guy?”
According to Mircea Mustaţă, Huh’s adviser at the University of Michigan, he required almost no supervision or guidance. Unlike most graduate students, he already had a program in mind, and ideas about how to pursue it. “He was more like a colleague,” Mustaţă said. “He already had his own way of looking at things.”
Many of his collaborators note that he’s incredibly humble and down-to-earth. When he learned he’d won the Fields Medal, “it didn’t really feel that good,” Huh said. “Of course you are happy, but deep down, you’re a little bit worried that they might eventually figure out that you’re not actually that good. I am a reasonably good mathematician, but am I Fields Medal-worthy?”
Escape From Space
Graphs are actually just one type of object that can define more general structures called matroids. Consider, for example, points on a two-dimensional plane. If more than two points lie on a line in this plane, you can say that those points are “dependent.” Matroids are abstract objects that capture notions like dependence and independence in all sorts of different contexts — from graphs to vector spaces to algebraic fields.
Just as graphs have chromatic polynomials associated with them, there are equations called characteristic polynomials attached to matroids. It was conjectured that the polynomials for these more general objects should also have coefficients that are log concave. But the techniques Huh used to prove Read’s conjecture only worked for showing log concavity for a very narrow class of matroids, such as the matroids that arise from graphs.
With the mathematician Eric Katz, Huh broadened the class of matroids such a proof could apply to. They followed a recipe of sorts. As before, the strategy was to start with the object of interest — here, a matroid — and use it to construct an algebraic variety. From there, they could extract an object called a cohomology ring and use some of its properties to prove log concavity.
There was just one problem. Most matroids don’t have any sort of geometric foundation, which means there’s not actually an algebraic variety to associate to them. Instead, Huh, Katz and the mathematician Karim Adiprasito figured out a way to write down the right cohomology ring straight from the matroid, essentially from scratch. They then showed, using a new set of techniques, that it behaved as if it had come from an actual algebraic variety, even though it hadn’t. In doing so, they proved log concavity for all matroids, resolving the problem known as Rota’s conjecture once and for all. “It’s pretty remarkable that it works,” Baker said.
The work showed that “you don’t need space to do geometry,” Huh said. “That made me really fundamentally rethink what geometry is.” It would also guide him toward a host of other problems, where he continued to push that idea further, allowing him to develop an even broader range of methods.
But for all the specificity the work requires, building the right cohomology ring requires massive amounts of guesswork and groping around in the dark. It was an aspect of the work that Huh particularly enjoyed. “There is no guiding principle … no clearly defined goal,” he said. “You just have to make a guess.”
Huh’s work involves investigating the properties of matroids. These abstract structures can sometimes arise from geometric objects. Caroline Gutman for Quanta Magazine
That lack of intention precisely mirrors how he functions best in his day-to-day life, too. It was as if he’d uncovered a mathematical program that perfectly fit his personality. Once again, he found that “things just happen by themselves,” Huh said.
The Heart of Things
Huh speaks slowly, pausing often and choosing his words carefully, and carries himself in a calm, peaceful manner that borders on meditative. “He doesn’t get so easily excited,” said Botong Wang, a mathematician at the University of Wisconsin, Madison who has collaborated with Huh on a number of important recent results.
He proceeds just as deliberately when doing mathematics. Wang was shocked when he first witnessed it. “I have this math competition experience, that as a mathematician you have to be clever, you have to be fast,” he said. “But June is the opposite. … If you talk to him for five minutes about some calculus problem, you’d think this guy wouldn’t pass a qualifying exam. He’s very slow.” So slow, in fact, that at first Wang thought they were wasting a lot of time on easy problems they already understood. But then he realized that Huh was learning even seemingly simple concepts in a much deeper way — and in precisely the way that would later prove useful.
“June likes to do things in the right way,” said Graham Denham, a mathematician at Western University in Ontario and one of Huh’s collaborators.
For instance, Denham, Ardila and Huh had just completed a 50-page proof of a problem closely related to Rota’s conjecture when Huh said they should take some more time to find a cleaner, more appealing approach. He thought there was a nicer explanation out there, and that it was best not to rush things. “Federico and I were like, oh, OK, so we’ll just chuck that, then, shall we?” Denham said.
It took two years to craft the better argument. “It’s good we’re all tenured,” Ardila said. Ultimately, though, Ardila and Denham agreed that the extra work was worth it. Their end result “was totally different, and deeper, and [got to] the heart of things,” Ardila said.
This approach doesn’t just apply to Huh’s mathematical work. In 2013, he decided he wanted to learn to cook. As a total beginner, he adopted the strategy of making the same dish — a simple pasta in oil — every day until it was perfect. For six months, that’s exactly what he did. (To date, according to Kim, that’s the only dish he knows how to cook.)
Huh’s entire life is built on routine. “Almost all of my days are exactly the same,” he said. “I have a very high tolerance for repetition.” He has trouble staying asleep and usually wakes up at around 3 a.m. He then goes to the gym, has breakfast with his wife and two sons (one is 8 years old, the other just turned 1), and walks his eldest to school before heading to his Princeton office.
The office is spare, practically empty. There’s a large desk, a couch for sleeping — Huh typically takes a nap later in the morning — and a yoga mat rolled out on the floor (just for lying down, he said; he doesn’t actually know how to do yoga). No books, just a few stacks of papers neatly arranged on a shelf against one wall. In the corner is a vacuum cleaner. Huh likes repetitive, mindless activities like cleaning, dishwashing and the physical act of transcribing what he reads into a notebook.
He often works in the public library, in the children’s section, where it’s pretty noisy. “I don’t like quiet places,” he said. “It makes me sleepy.” Huh says this about many things.
He goes for a long walk after lunch each day, then returns to his office to do some more work (unless he’s already hit his three-hour quota) before heading home. He spends the rest of the evening with his family; they all go to sleep, together in one large bed, at around 9 p.m.
This preference for routine — and the tendency to get exhausted by anything that strays from it — can sometimes manifest in extreme ways. When he was completing his doctorate in Michigan, for instance, “I would cut off almost everything else,” Huh said. When he first moved to Ann Arbor, he found himself unequipped for the brutal winter. He had few belongings, and he needed a blanket. But when he looked up how to get to the local mall, he found it too logistically difficult. “It was just beyond my level of tolerance,” he said. “I did not want to waste my mental energy on figuring out how to go from here to there.” Instead, he walked to a nearby CVS drugstore, bought 10 squares of fabric and a giant stapler, and stapled the squares together to make a blanket.

Huh in Princeton’s Lewis Science Library. Caroline Gutman for Quanta Magazine
He lived off frozen pizza for months at a time because he didn’t want to deal with getting groceries and cooking. He just wanted to do math. He describes that period of his life as “almost monastic.” In fact, at the time, he really only spoke with another person — Mustaţă, his adviser — once a week.
Kim recalls visiting Huh when he was still in Illinois, and “after that, I really rethought our relationship,” she said. “Should I marry him? Because he [cannot] handle real-life skills, surviving skills.”
Yet marry him she did, in 2014. They moved to Princeton, where they both started work at the Institute for Advanced Study. It was Kim’s first time living in the U.S., and she felt uncomfortable taking care of certain tasks in English; she had to depend on Huh to get things done. “Let’s just say, she was disappointed,” he said.
Later that year, Kim gave birth to their first son, Dan. While in labor, she caught Huh doing math.
“My wife is a much more balanced person than I am,” he said. “Life has very many facets, and math is a very, very, very tiny part of it.”
“I’m a real worker,” Kim said. “He is a thinker.”
But, she added, Huh has improved drastically since then. As the couple raised Dan, “I learned how to live a more balanced life,” Huh said. “That was a transformative period.” He spends a lot of time with Dan — drawing with him, solving problems in intricate math workbooks that Dan creates for him, and taking him to the bookstore and other local spots. He even takes care of the logistical tasks that Kim asks him to do, albeit begrudgingly. “I still don’t like it,” he said, “but I mean, we cannot just live with stapled blankets.”
Now he’s even able to step away from mathematics. His mind no longer returns to working on problems when he’s in an idle state, and he’s able to take a break when something else requires him to.
“He’s a totally different person,” Kim said.
Heavy on Top
Regardless, some things haven’t changed. Huh can still muster only enough energy to work for a few hours each day. “Other people work one hour and just take a five-minute rest,” Kim said. “He is like, one hour do something else, and just focus for five minutes, 10 minutes.”
His search for beauty hasn’t changed either. And often he returns to questions about log concavity or similar concepts as a way to unearth that beauty.
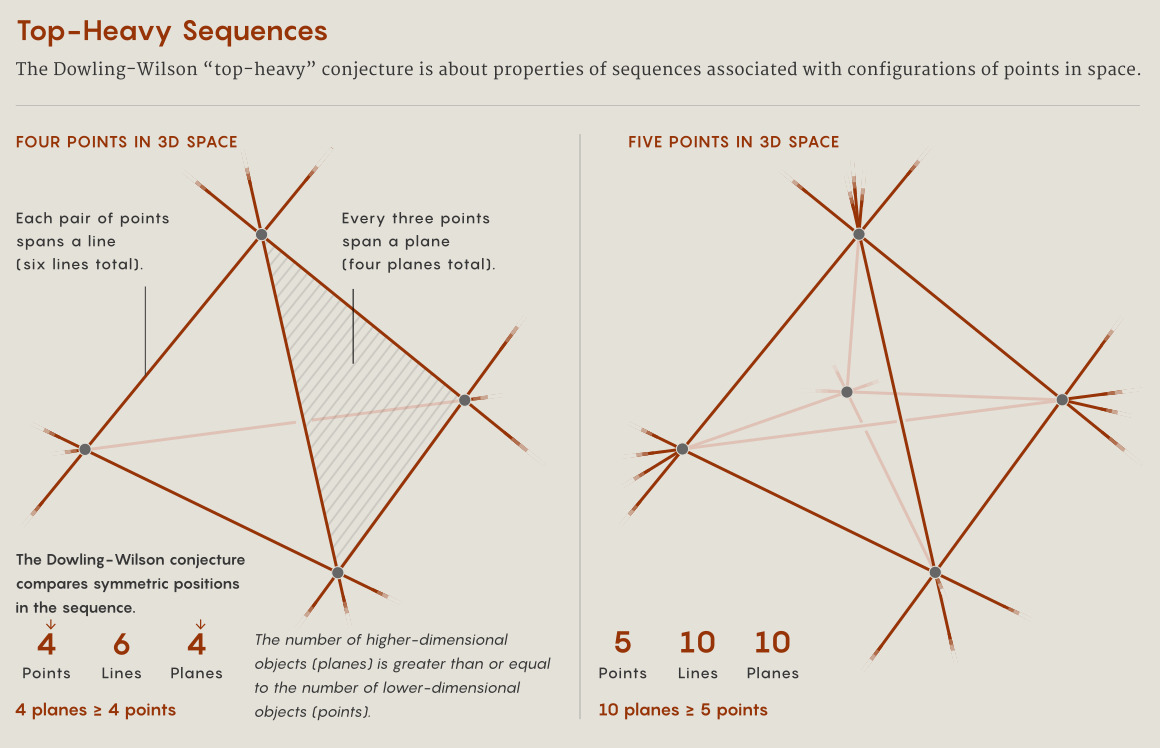
For instance, he, Wang and other collaborators recently proved a fundamental problem about configurations of points, lines and planes called the Dowling-Wilson “top-heavy” conjecture. Consider a finite collection of points in the plane, where every pair of points is connected by a line. The mathematicians Paul Erdős and Nicolaas Govert de Bruijn showed that the number of lines must always be greater than or equal to the number of points (unless all the points are located on one line). Consider, for example, four points arranged at the corners of a square. Lines trace out the square and also connect opposite corners, adding up to six lines in total.
The top-heavy conjecture generalizes this idea. Instead of the plane, you’re given a set of points in some high-dimensional space. Consider all the lines that connect pairs of points, the planes spanned by sets of three points, the three-dimensional subspaces constructed from four points, and so on. Now think about a sequence built from these numbers: the number of points, the number of lines, the number of planes. Compare numbers in symmetric positions in that sequence (the first and last numbers, the second and penultimate numbers, and so on). The number corresponding to the higher-dimensional space will be at least as large — that is, the sequence is top-heavy. (This sequence is also conjectured to be log concave, but that has not yet been proved; so far, Huh and Wang have shown that the first half of the sequence is unimodal.)
Merrill Sherman/Quanta Magazine
Huh and Wang adapted ideas from Huh’s work on Rota’s conjecture, but in doing so they had to push his program further. Again, they were working with matroids, algebraic varieties and cohomology rings. But this time the algebraic varieties they had to find involved singularities, places where a space looks different when you zoom in on it than it does at other points. That made it much more complicated to build the right spaces and prove certain properties about their cohomology rings — and even more difficult to solve the case where they had to construct those rings straight from the matroids, without algebraic varieties to guide them.
During the five years they spent solving this problem, Huh also started investigating a way to complete the break from geometry. So much of his work until then involved the arduous task of building the exact cohomology that a problem required. Moreover, once that cohomology is found, mathematicians still have to prove that it satisfies certain properties, which can also take years.

Caroline Gutman for Quanta Magazine
The new theory that he developed (along with the mathematician Petter Brändén) was able to bypass those methods entirely. It allowed them to solve a problem called the strong Mason conjecture (which asks questions about the number of independent sets in matroids), and other mathematicians have already used it to re-prove Rota’s conjecture in a more straightforward way. But even more important, it opens the door to finding entirely new problems, hints at an even deeper explanation for why all these log concavity statements are true, and intersects with problems in theoretical computer science in intriguing ways that are just beginning to be explored.
Click of the Connection
For Huh, when he is working, there’s something almost subconscious going on. In fact, he usually can’t trace how or when his ideas come to him. He doesn’t have sudden flashes of insight. Instead, “at some point, you just realize, oh, I know this,” he said. Maybe last week, he didn’t understand something, but now, without any additional input, the pieces have clicked into place without his realizing it. He likens it to the way your mind can surprise you and create unexpected connections when you’re dreaming. “It’s just amazing what human minds are capable of,” he said. “And it’s nice to admit that we don’t know what’s going on.”
Perhaps this, too, speaks to the artist in him. He hopes to continue uncovering unexpected connections between different areas of math.
“He just follows the vision of this original program that he had … already as a graduate student,” Baker said. “It will be very interesting to see what the limits are.”
So far, Huh hasn’t hit them. And mathematicians are sure he’ll continue to make beautiful things.
When asked if he’d ever entertain the earlier version of his artist self and try writing poetry again, he shrugged. “Maybe. But I don’t know,” he said. “I’m very much into something else.”
'제일 기분좋게하는 오늘의 기사' 카테고리의 다른 글
| 한국 최저임금 일본 넘었다…내년 韓 9620원 vs 日 9509원 (0) | 2022.08.02 |
|---|---|
| 우크라전 놀란 폴란드 무기 3종 구매…K방산에 초대박 안겼다 (0) | 2022.07.27 |
| 이재용·정의선도 나섰다… 빈살만의 640조원 ‘네옴시티’ 수주戰 (0) | 2022.06.29 |
| 한국 최초 美 물리학회장 된 ‘충돌의 여왕’… “유리 천장? 일단 부딪쳐봐” (0) | 2022.06.18 |
| 한국의 매력, 천시를 만나다 (0) | 2022.06.14 |