Writing away at my desk, I reach my hand up to turn on a lamp, and down to open a drawer to take out a pen. Extending my arm forward, I brush my fingers against a small, strange figurine given to me by my sister as a good-luck charm, while reaching behind I can pat the black cat snuggling into my back. Right leads to the research notes for my article, left to my pile of ‘must-do’ items (bills and correspondence). Up, down, forward, back, right, left: I pilot myself in a personal cosmos of three-dimensional space, the axes of this world invisibly pressed upon me by the rectilinear structure of my office, defined, like most Western architecture, by three conjoining right angles.
Our architecture, our education and our dictionaries tell us that space is three-dimensional. The OED defines it as ‘a continuous area or expanse which is free, available or unoccupied … The dimensions of height, depth and width, within which all things exist and move.’ In the 18th century, Immanuel Kant argued that three-dimensional Euclidean space is an a priori necessity and, saturated as we are now in computer-generated imagery and video games, we are constantly subjected to representations of a seemingly axiomatic Cartesian grid. From the perspective of the 21st century, this seems almost self-evident.
Yet the notion that we inhabit a space with any mathematical structure is a radical innovation of Western culture, necessitating an overthrow of long-held beliefs about the nature of reality. Although the birth of modern science is often discussed as a transition to a mechanistic account of nature, arguably more important – and certainly more enduring – is the transformation it entrained in our conception of space as a geometrical construct.
Over the past century, the quest to describe the geometry of space has become a major project in theoretical physics, with experts from Albert Einstein onwards attempting to explain all the fundamental forces of nature as byproducts of the shape of space itself. While on the local level we are trained to think of space as having three dimensions, general relativity paints a picture of a four-dimensional universe, and string theory says it has 10 dimensions – or 11 if you take an extended version known as M-Theory. There are variations of the theory in 26 dimensions, and recently pure mathematicians have been electrified by a version describing spaces of 24 dimensions. But what are these ‘dimensions’? And what does it mean to talk about a 10-dimensional space of being?
In order to come to the modern mathematical mode of thinking about space, one first has to conceive of it as some kind of arena that matter might occupy. At the very least, ‘space’ has to be thought of as something extended. Obvious though this might seem to us, such an idea was anathema to Aristotle, whose concepts about the physical world dominated Western thinking in late antiquity and the Middle Ages.
Strictly speaking, Aristotelian physics didn’t include a theory of space, only a concept of place. Think of a cup sitting on a table. For Aristotle, the cup is surrounded by air, itself a substance. In his world picture, there is no such thing as empty space, there are only boundaries between one kind of substance, the cup, and another, the air. Or the table. For Aristotle, ‘space’ (if you want to call it that), was merely the infinitesimally thin boundary between the cup and what surrounds it. Without extension, space wasn’t something anything else could be in.
Centuries before Aristotle, Leucippus and Democritus had posited a theory of reality that invoked an inherently spatialised way of seeing – an ‘atomistic’ vision, whereby the material world is composed of minuscule particles (or atoms) moving through a void. But Aristotle rejected atomism, claiming that the very concept of a void was logically incoherent. By definition, he said, ‘nothing’ cannot be. Overcoming Aristotle’s objection to the void, and thus to the concept of extended space, would be a project of centuries. Not until Galileo and Descartes made extended space one of the cornerstones of modern physics in the early 17th century does this innovative vision come into its own. For both thinkers, as the American philosopher Edwin Burtt put it in 1924, ‘physical space was assumed to be identical with the realm of geometry’ – that is, the three-dimensional Euclidean geometry we are now taught in school.
Long before physicists embraced the Euclidean vision, painters had been pioneering a geometrical conception of space, and it is to them that we owe this remarkable leap in our conceptual framework. During the late Middle Ages, under a newly emerging influence deriving from Plato and Pythagoras, Aristotle’s prime intellectual rivals, a view began to percolate in Europe that God had created the world according to the laws of Euclidean geometry. Hence, if artists wished to portray it truly, they should emulate the Creator in their representational strategies. From the 14th to the 16th centuries, artists such as Giotto, Paolo Uccello and Piero della Francesca developed the techniques of what came to be known as perspective – a style originally termed ‘geometric figuring’. By consciously exploring geometric principles, these painters gradually learned how to construct images of objects in three-dimensional space. In the process, they reprogrammed European minds to see space in a Euclidean fashion.
The historian Samuel Edgerton recounts this remarkable segue into modern science in The Heritage of Giotto’s Geometry (1991), noting how the overthrow of Aristotelian thinking about space was achieved in part as a long, slow byproduct of people standing in front of perspectival paintings and feeling, viscerally, as if they were ‘looking through’ to three-dimensional worlds on the other side of the wall. What is so extraordinary here is that, while philosophers and proto-scientists were cautiously challenging Aristotelian precepts about space, artists cut a radical swathe through this intellectual territory by appealing to the senses. In a very literal fashion, perspectival representation was a form of virtual reality that, like today’s VR games, aimed to give viewers the illusion that they had been transported into geometrically coherent and psychologically convincing other worlds.
The structure of the ‘real’ went from a philosophical and theological question to a geometrical proposition
The illusionary Euclidean space of perspectival representation that gradually imprinted itself on European consciousness was embraced by Descartes and Galileo as the space of the real world. Worth adding here is that Galileo himself was trained in perspective. His ability to represent depth was a critical feature in his groundbreaking drawings of the Moon, which depicted mountains and valleys and implied that the Moon was as solidly material as the Earth.
By adopting the space of perspectival imagery, Galileo could show how objects such as cannonballs moved according to mathematical laws. The space itself was an abstraction – a featureless, inert, untouchable, un-sensable void, whose only knowable property was its Euclidean form. By the end of the 17th century, Isaac Newton had expanded this Galilean vision to encompass the universe at large, which now became a potentially infinite three-dimensional vacuum – a vast, quality-less, emptiness extending forever in all directions. The structure of the ‘real’ had thus been transformed from a philosophical and theological question into a geometrical proposition.
Where painters had used mathematical tools to develop new ways of making images, now, at the dawn of the ‘scientific revolution’, Descartes discovered a way to make images of mathematical relations in and of themselves. In the process, he formalised the concept of a dimension, and injected into our consciousness not only a new way of seeing the world but a new tool for doing science.
Almost everyone today recognises the fruits of Descartes’s genius in the image of the Cartesian plane – a rectangular grid marked with an x and y axis, and a coordinate system.
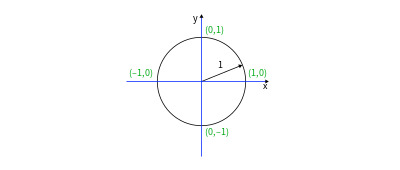
By definition, the Cartesian plane is a two-dimensional space because we need two coordinates to identify any point within it. Descartes discovered that with this framework he could link geometric shapes and equations. Thus, a circle with a radius of 1 can be described by the equation x2 + y2 =1.
A vast array of figures that we can draw on this plane can be described by equations, and such ‘analytic’ or ‘Cartesian’ geometry would soon become the basis for the calculus developed by Newton and G W Leibniz to further physicists’ analysis of motion. One way to understand calculus is as the study of curves; so, for instance, it enables us to formally define where a curve is steepest, or where it reaches a local maximum or minimum. When applied to the study of motion, calculus gives us a way to analyse and predict where, for instance, an object thrown into the air will reach a maximum height, or when a ball rolling down a curved slope will reach a specific speed. Since its invention, calculus has become a vital tool for almost every branch of science.
Considering the previous diagram, it’s easy to see how we can add a third axis. Thus with an x, y and z axis, we can describe the surface of a sphere – as in the skin of a beach ball. Here the equation (for a sphere with a radius of 1 ) becomes: x2 + y2 + z2 = 1
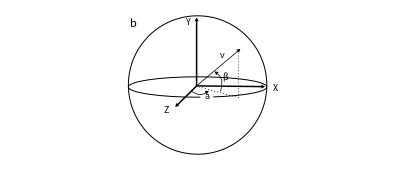
With three axes, we can describe forms in three-dimensional space. And again, every point is uniquely identified by three coordinates: it’s the necessary condition of three-ness that makes the space three-dimensional.
But why stop there? What if I add a fourth dimension? Let’s call it ‘p’. Now I can write an equation for something I claim is a sphere sitting in four-dimensional space: x2 + y2 + z2 + p2 = 1. I can’t draw this object for you, yet mathematically the addition of another dimension is a legitimate move. ‘Legitimate’ meaning there’s nothing logically inconsistent about doing so – there’s no reason I can’t.
A ‘dimension’ becomes a purely symbolic concept not necessarily linked to the material world at all
And I can keep on going, adding more dimensions. So I define a sphere in five-dimensional space with five coordinate axes (x, y, z, p, q) giving us the equation: x2 + y2 + z2+ p2 + q2 = 1. And one in six-dimensions: x2 + y2 + z2 + p2 + q2 + r2 = 1, and so on.
Although I might not be able to visualise higher-dimensional spheres, I can describe them symbolically, and one way of understanding the history of mathematics is as an unfolding realisation about what seemingly sensible things we can transcend. This is what Charles Dodgson, aka Lewis Carroll, was getting at when, in Through the Looking Glass, and What Alice Found There (1871), he had the White Queen assert her ability to believe ‘six impossible things before breakfast’.
Mathematically, I can describe a sphere in any number of dimensions I choose. All I have to do is keep adding new coordinate axes, what mathematicians call ‘degrees of freedom’. Conventionally, they are named x1, x2, x3, x4, x5, x6 et cetera. Just as any point on a Cartesian plane can be described by two (x, y) coordinates, so any point in a 17-dimensional space can be described by set of 17 coordinates (x1, x2, x3, x4, x5, x6 … x15, x16, x17). Surfaces like the spheres above, in such multidimensional spaces, are generically known as manifolds.
From the perspective of mathematics, a ‘dimension’ is nothing more than another coordinate axis (another degree of freedom), which ultimately becomes a purely symbolic concept not necessarily linked at all to the material world. In the 1860s, the pioneering logician Augustus De Morgan, whose work influenced Lewis Carroll, summed up the increasingly abstract view of this field by noting that mathematics is purely ‘the science of symbols’, and as such doesn’t have to relate to anything other than itself. Mathematics, in a sense, is logic let loose in the field of the imagination.
Unlike mathematicians, who are at liberty to play in the field of ideas, physics is bound to nature, and at least in principle, is allied with material things. Yet all this raises a liberating possibility, for if mathematics allows for more than three dimensions, and we think mathematics is useful for describing the world, how do we know that physical space is limited to three? Although Galileo, Newton and Kant had taken length, breadth and height to be axiomatic, might there not be more dimensions to our world?
Again, the idea of a universe with more than three dimensions was injected into public consciousness through an artistic medium, in this case literary speculation, most famously in the mathematician Edwin A Abbott’s Flatland (1884). This enchanting social satire tells the story of a humble Square living on a plane, who is one day visited by a three-dimensional being, Lord Sphere, who propels him into the magnificent world of Solids. In this volumetric paradise, Square beholds a three-dimensional version of himself, the Cube, and begins to dream of pushing on to a fourth, fifth and sixth dimension. Why not a hypercube? And a hyper-hypercube, he wonders?
Sadly, back in Flatland, Square is deemed a lunatic, and locked in an insane asylum. One of the virtues of the story, unlike some of the more saccharine animations and adaptations it has inspired, is its recognition of the dangers entailed in flaunting social convention. While Square is arguing for other dimensions of space, he is also making a case for other dimensions of being – he’s a mathematical queer.
In the late 19th and early 20th centuries, a raft of authors (H G Wells, the mathematician and sci-fi writer Charles Hinton, who coined the word ‘tesseract’ for the 4D cube), artists (Salvador Dalí) and mystical thinkers (P D Ouspensky), explored ideas about the fourth dimension and what it might mean for humans to encounter it.
Then in 1905, an unknown physicist named Albert Einstein published a paper describing the real world as a four-dimensional setting. In his ‘special theory of relativity’, time was added to the three classical dimensions of space. In the mathematical formalism of relativity, all four dimensions are bound together, and the term spacetime entered our lexicon. This assemblage was by no means arbitrary. Einstein found that, by going down this path, a powerful mathematical apparatus came into being that transcended Newton’s physics and enabled him to predict the behaviour of electrically charged particles. Only in a 4D model of the world can electromagnetism be fully and accurately described.
Relativity was a great deal more than another literary game, especially once Einstein extended it from the ‘special’ to the ‘general’ theory. Now multidimensional space became imbued with deep physical meaning.
In Newton’s world picture, matter moves through space in time under the influence of natural forces, particularly gravity. Space, time, matter and force are distinct categories of reality. With special relativity, Einstein demonstrated that space and time were unified, thus reducing the fundamental physical categories from four to three: spacetime, matter and force. General relativity takes a further step by enfolding the force of gravity into the structure of spacetime itself. Seen from a 4D perspective, gravity is just an artifact of the shape of space.
To comprehend this remarkable situation, let’s imagine for the moment its two-dimensional analogue. Think of a trampoline, and imagine we draw on its surface a Cartesian grid. Now put a bowling ball onto the grid. Around it, the surface will stretch and warp so some points become further away from each other. We’ve disturbed the inherent measure of distance within the space, making it uneven. General relativity says that this warping is what a heavy object, such as the Sun, does to spacetime, and the aberration from Cartesian perfection of the space itself gives rise to the phenomenon we experience as gravity.
Whereas in Newton’s physics, gravity comes out of nowhere, in Einstein’s it arises naturally from the inherent geometry of a four-dimensional manifold; in places where the manifold stretches most, or deviates most from Cartesian regularity, gravity feels stronger. This is sometimes referred to as ‘rubber-sheet physics’. Here, the vast cosmic force holding planets in orbit around stars, and stars in orbit around galaxies, is nothing more than a side-effect of warped space. Gravity is literally geometry in action.
If moving into four dimensions helps to explain gravity, then might thinking in five dimensions have any scientific advantage? Why not give it a go? a young Polish mathematician named Theodor Kaluza asked in 1919, thinking that if Einstein had absorbed gravity into spacetime, then perhaps a further dimension might similarly account for the force of electromagnetism as an artifact of spacetime’s geometry. So Kaluza added another dimension to Einstein’s equations, and to his delight found that in five dimensions both forces fell out nicely as artifacts of the geometric model.
You’re an ant running on a long, thin hose, without ever being aware of the tiny circle-dimension underfoot
The mathematics fit like magic, but the problem in this case was that the additional dimension didn’t seem to correlate with any particular physical quality. In general relativity, the fourth dimension was time; in Kaluza’s theory, it wasn’t anything you could point to, see, or feel: it was just there in the mathematics. Even Einstein balked at such an ethereal innovation. What is it? he asked. Where is it?
In 1926, the Swedish physicist Oskar Klein answered this question in a way that reads like something straight out of Wonderland. Imagine, he said, you are an ant living on a long, very thin length of hose. You could run along the hose backward and forward without ever being aware of the tiny circle-dimension under your feet. Only your ant-physicists with their powerful ant-microscopes can see this tiny dimension. According to Klein, every point in our four-dimensional spacetime has a little extra circle of space like this that’s too tiny for us to see. Since it is many orders of magnitude smaller than an atom, it’s no wonder we’ve missed it so far. Only physicists with super-powerful particle accelerators can hope to see down to such a minuscule scale.
Once physicists got over their initial shock, they became enchanted by Klein’s idea, and during the 1940s the theory was elaborated in great mathematical detail and set into a quantum context. Unfortunately, the infinitesimal scale of the new dimension made it impossible to imagine how it could be experimentally verified. Klein calculated that the diameter of the tiny circle was just 10-30 cm. By comparison, the diameter of a hydrogen atom is 10-8 cm, so we’re talking about something more than 20 orders of magnitude smaller than the smallest atom. Even today, we’re nowhere close to being able to see such a minute scale. And so the idea faded out of fashion.
Kaluza, however, was not a man easily deterred. He believed in his fifth dimension, and he believed in the power of mathematical theory, so he decided to conduct an experiment of his own. He settled on the subject of swimming. Kaluza could not swim, so he read all he could about the theory of swimming, and when he felt he’d absorbed aquatic exercise in principle, he escorted his family to the seaside and hurled himself into the waves, where lo and behold he could swim. In Kaluza’s mind, the swimming experiment upheld the validity of theory and, though he did not live to see the triumph of his beloved fifth dimension, in the 1960s string theorists resurrected the idea of higher-dimensional space.
By the 1960s, physicists had discovered two additional forces of nature, both operating at the subatomic scale. Called the weak nuclear force and the strong nuclear force, they are responsible for some types of radioactivity and for holding quarks together to form the protons and neutrons that make up atomic nuclei. In the late 1960s, as physicists began to explore the new subject of string theory (which posits that particles are like minuscule rubber bands vibrating in space), Kaluza’s and Klein’s ideas bubbled back into awareness, and theorists gradually began to wonder if the two subatomic forces could also be described in terms of spacetime geometry.
It turns out that in order to encompass both of these two forces, we have to add another five dimensions to our mathematical description. There’s no a priori reason it should be five; and, again, none of these additional dimensions relates directly to our sensory experience. They are just there in the mathematics. So this gets us to the 10 dimensions of string theory. Here there are the four large-scale dimensions of spacetime (described by general relativity), plus an extra six ‘compact’ dimensions (one for electromagnetism and five for the nuclear forces), all curled up in some fiendishly complex, scrunched-up, geometric structure.
A great deal of effort is being expended by physicists and mathematicians to understand all the possible shapes that this miniature space might take, and which, if any, of the many alternatives is realised in the real world. Technically, these forms are known as Calabi-Yau manifolds, and they can exist in any even number of higher dimensions. Exotic, elaborate creatures, these extraordinary forms constitute an abstract taxonomy in multidimensional space; a 2D slice through them (about the best we can do in visualising what they look like) brings to mind the crystalline structures of viruses; they almost look alive.

There are many versions of string-theory equations describing 10-dimensional space, but in the 1990s the mathematician Edward Witten, at the Institute for Advanced Study in Princeton (Einstein’s old haunt), showed that things could be somewhat simplified if we took an 11-dimensional perspective. He called his new theory M-Theory, and enigmatically declined to say what the ‘M’ stood for. Usually it is said to be ‘membrane’, but ‘matrix’, ‘master’, ‘mystery’ and ‘monster’ have also been proposed.
Ours might be just one of many co-existing universes, each a separate 4D bubble in a wider arena of 5D space
So far, we have no evidence for any of these additional dimensions – we are still in the land of swimming physicists dreaming of a miniature landscape we cannot yet access – but string theory has turned out to have powerful implications for mathematics itself. Recently, developments in a version of the theory that has 24 dimensions has shown unexpected interconnections between several major branches of mathematics, which means that, even if string theory doesn’t pan out in physics, it will have proven a richly rewarding source of purely theoretical insight. In mathematics, 24-dimensional space is rather special – magical things happen there, such as the ability to pack spheres together in a particularly elegant way – though it’s unlikely that the real world has 24 dimensions. For the world we love and live in, most string theorists believe that 10 or 11 dimensions will prove sufficient.
There is one final development in string theory that warrants attention. In 1999, Lisa Randall (the first woman to get tenure at Harvard as a theoretical physicist) and Raman Sundrum (an Indian-American particle theorist) proposed that there might be an additional dimension on the cosmological scale, the scale described by general relativity. According to their ‘brane’ theory – ‘brane’ being short for ‘membrane’ – what we normally call our Universe might be embedded in a vastly bigger five-dimensional space, a kind of super-universe. Within this super-space, ours might be just one of a whole array of co-existing universes, each a separate 4D bubble within a wider arena of 5D space.
It is hard to know if we’ll ever be able to confirm Randall and Sundrum’s theory. However analogies have been drawn between this idea and the dawn of modern astronomy. Europeans 500 years ago found it impossible to imagine other physical ‘worlds’ beyond our own, yet now we know that the Universe is populated by billions of other planets orbiting around billions of other stars. Who knows, one day our descendants could find evidence for billions of other universes, each with their own unique spacetime equations.
The project of understanding the geometrical structure of space is one of the signature achievements of science, but it might be that physicists have reached the end of this road. For it turns out that, in a sense, Aristotle was right – there are indeed logical problems with the notion of extended space. For all the extraordinary successes of relativity, we know that its description of space cannot be the final one because at the quantum level it breaks down. For the past half-century, physicists have been trying without success to unite their understanding of space at the cosmological scale with what they observe at the quantum scale, and increasingly it seems that such a synthesis could require radical new physics.
After Einstein developed general relativity, he spent much of the rest of his life trying to ‘build all of the laws of nature out of the dynamics of space and time, reducing physics to pure geometry’, as Robbert Dijkgraaf, director of the Institute for Advanced Study at Princeton, put it recently. ‘For [Einstein], space-time was the natural “ground-level” in the infinite hierarchy of scientific objects.’ Like Newton’s world picture, Einstein’s makes space the primary grounding of being, the arena in which all things happen. Yet at very tiny scales, where quantum properties dominate, the laws of physics reveal that space, as we are used to thinking about it, might not exist.
A view is emerging among some theoretical physicists that space might in fact be an emergent phenomenon created by something more fundamental, in much the same way that temperature emerges as a macroscopic property resulting from the motion of molecules. As Dijkgraaf put it: ‘The present point of view thinks of space-time not as a starting point, but as an end point, as a natural structure that emerges out of the complexity of quantum information.’
A leading proponent of new ways of thinking about space is the cosmologist Sean Carroll at Caltech, who recently said that classical space isn’t ‘a fundamental part of reality’s architecture’, and argued that we are wrong to assign such special status to its four or 10 or 11 dimensions. Where Dijkgraaf makes an analogy with temperature, Carroll invites us to consider ‘wetness’, an emergent phenomenon of lots of water molecules coming together. No individual water molecule is wet, only when you get a bunch of them together does wetness come into being as a quality. So, he says, space emerges from more basic things at the quantum level.
Carroll writes that, from a quantum perspective, the Universe ‘evolves in a mathematical realm with more than 10(10^100) dimensions’ – that’s 10 followed by a googol of zeroes, or 10,000 trillion trillion trillion trillion trillion trillion trillion trillion zeroes. It’s hard to conceive of this almost impossibly vast number, which dwarfs into insignificance the number of particles in the known Universe. Yet every one of them is a separate dimension in a mathematical space described by quantum equations; every one a new ‘degree of freedom’ that the Universe has at its disposal.
Even Descartes might have been stunned by where his vision has taken us, and what dazzling complexity has come to be contained in the simple word ‘dimension’.
This Essay was made possible through the support of a grant to Aeon magazine from Templeton Religion Trust. The opinions expressed in this publication are those of the author(s) and do not necessarily reflect the views of Templeton Religion Trust.
Funders to Aeon Magazine are not involved in editorial decision-making, including commissioning or content approval.
